做多級的RF的放大器時，除了看一般的stability factor K值外，還需要去測試電路每級放大器的級間穩定。
實驗室一直遵照學長流傳下來的投影片：將電路從中切開，一邊看stability circle，另一邊看ADS裡面的「Map1 circle」跟「Map2 circle」這個東西，然後看看兩個圓有沒有相交在一起，可是這個Map 1/2 circle是啥鬼東西？極間穩定又是什麼？

極間穩定的意義

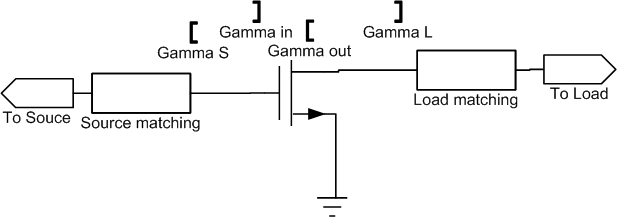stage_stability 先考慮上圖的模型，在一個主動的電晶體兩旁接上matching的電路，stability circle的定義是：

在什麼樣的 $\Gamma_L$ 或 $\Gamma_S$ 下，會讓 $\Gamma_{in}(out) > 1$，在$\Gamma_{in}(out) > 1$時，電路幾乎確定會不穩定，將 $\Gamma_{in}(out)=1$ 的邊線畫出來的圓，就是穩定圓(stability circle)。

電路設計完後，一定會看看 stability factor K是否全頻帶都大於1，就是要確認電路整體的 $\Gamma_{in}(out)$ 都在穩定的範圍內。

可是若我們把電路切開，這個模型就不適用了，前後接的不是被動的matching電路，這時候我們就要確保，前端的load stability circle，和向後端可能看到任何一點阻抗，都不會相交；否則很不巧的該阻抗出現，電路就不穩定了；這就是極間穩定背後的原理。

所以說map1/2 circle是啥鬼？從上面的定義來看，我認為它所畫的是：當source(load)呈現任何被動阻抗時（也就是實部小於一，落在smith chart上的任何阻抗），會在另一邊load(source)上呈現的阻抗。
實際用複數變換來驗證看看：

$$\Gamma_{in} = w = \frac{a \Gamma_L+b}{c\Gamma_L+d}$$

改換上式為下式，兩行的abcd並不是相同的：

$$\Gamma_L = \frac{a \Gamma_{in}+b}{c \Gamma_{in}+d}$$

$$a=1, b= -S_{11}, c= S_{22}, d= -\Delta$$

其中 $$\Delta = S_{11}S_{22}-S_{12}S_{21}$$

這個 $|\Gamma_L|=1$ 經轉換後會畫出一個圓，其圓心和半徑為：

$$C_L = \frac{\bar{c}d-\bar{a}b}{a^2-c^2} = \frac{-S_{11}|S_{22}^2|+S_{12}S_{21}\bar{S_{22}}+S_{11}}{1-|S_{22}|^2} = S_{11}+\frac{S_{12}S_{21}\bar{S_{22}}}{1-|S_{22}|^2}$$

$$r = \frac{ad-bc}{a^2-c^2} = |\frac{S_{12}S_{21}}{1-|S_{22}|^2}|$$

若兩圓相交，就表示有load會讓 $\Gamma_L$ 呈現某阻抗，而該阻抗會落在不穩定圓中，也就使電路在這級不穩定(新細明體：你死了Q_Q)

實際資料

Linux有問題先查manpage，ADS遇到鬼先問F1 help，結果help裡面解釋是這麼寫的：

Used in Small-signal S-parameter simulations: The function maps the set of terminations with unity magnitude at port 1 to port 2. The circles are defined by the loci of terminations on one port as seen at the other port. A source-mapping circle is created for each value of the swept variable(s). This measurement is supported for 2-port networks only.

大概的意思是一樣的，依著help的註解找到了計算的ael原始碼，下面是map2的原始碼：

defun map2_center_and_radius(sParam, center, radius)
{
    decl S12xS21 = sParam(1,2)*sParam(2,1);
    decl s11MagSq = pow(abs(sParam(1,1)),2);
     *center = sParam(2,2)+S12xS21*conj(sParam(1,1))/(1-s11MagSq);
     *radius = abs(S12xS21)/(1-s11MagSq);
}

可見所做的是以

$$S_{11}+\frac{S_{12}S_{21}\bar{S_{22}}}{1-|S22|^2}$$

為圓心

$$|\frac{S_{12}S_{21}}{1-|S22|^2}|$$

為半徑的圓，和我們所計算的結果相符。

更正：我算的跟他的剛好是反過來的，我算的應該是 map1 的結果。

致謝

本篇文章感謝503實驗室強者我同學曾奕恩，以及強者我學長陳柏翰學長在複數變換方面的指導。

極間穩定的意義#

實際資料#

致謝#

極間穩定的意義

實際資料

致謝