最近費式數列實在有點紅,讓小弟忍不住也來玩一下。
費式數列給一個初學程式的人都能寫得出來,例如早年我忘了哪位大大在推坑我 python 的時候,就寫了個只要 4 行列出費氏數列的 python 程式,一方面展現 python 在大數運算上的實力,一方面展視了它的簡潔,像是 a , b = a+b, a 這種寫法。
a = b = 1
while b < 1000000000000:
print(b)
a, b = a+b, a
當然會寫是一回事,深入進去就沒那麼簡單了,詳細請參考這個網頁
。
最簡單、最直覺的遞迴寫法,但這其實是會噴射的,每次遞迴都會做重複的計算,於是計算以指數的方式成長,
比如說我用 python 的 timeit 去測一個遞迴的費式數列函式,很快執行時間就會爆炸,大概到了 fib(30) 以上就會跑得很吃力了。
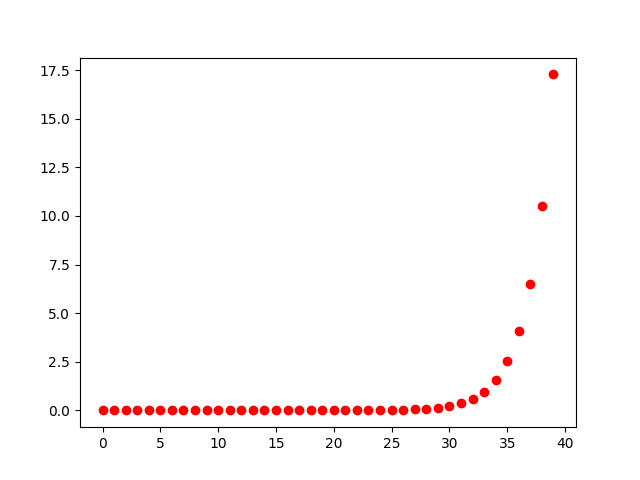
如果我們用單純的加法,從 1 開始往上加,其實只要進行 n 次的加法就能得到 fib(n) 了,執行複雜度為 O(n);如果再套用更快的 fast fibonacci,更可以把執行時間拉到 O(lg n) 的程度,只要 fib(94) 就超過 64 bits 的整數的情況下,用 O(lg n) 的演算法其實跟常數時間所差無幾。
不過呢,費式數列還有一個公式解呢,也就是:
$$ fib(n) = \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n-\frac{1}{\sqrt{5}}(\frac{1-\sqrt{5}}{2})^n $$
為什麼不用這個算式算呢?公式解不是常數時間嗎?
數學上來說:是的,但實際上會遇上一些問題,例如我們看看 64 bits 整數裡面最大的 fib(93) 為例,整數算的解為:
12200160415121876738
如果是 python 寫的公式解呢?
def fib(n):
return (math.pow((1+math.sqrt(5))/2, n) - math.pow((1-math.sqrt(5))/2, n)) / math.sqrt(5)
print(int(fib(93)))
12200160415121913856
登登,問題大條了,答案不一樣。
何以致此,問題就來到浮點數的不精確問題,這時候就要先來一張經典的漫畫了:

我們在計算完 sqrt(5) 之後,只能用一個近似的值來表達結果,在 python 內預設是以雙精度浮點數在儲存, 它跟真正的 sqrt(5) 還是有細微的差距,在隨後的 n 次方、除法上,這個細微的誤差都會被慢慢的放大,最終導致這個巨大的誤差。
幸好我們不是沒有解法的,參考了 C/C++ 版上,傳說中的 Schottky 大大曾經分享如何使用 gmp 或 mpfr 兩個函式庫,算出
這兩個 gnu 函式庫是所謂的無限位數的整數跟無限精確度的浮點數,當然他們不是真的無限,只是完全壓榨記憶體來記錄儘可能多的位數以求精確, 理論上記憶體撐上去就能把精確度逼上去,只是有沒有那個必要就是,像是把一些無理數算到一億位(欸。
究竟這個函式庫有多麼的強大呢?我們可以來寫個簡單的,例如來算個黃金比例,只要這樣就結束了:
mpfr_t phi;
unsigned long int precision, x=5;
uint64_t digits = DIGITS;
precision = ceill((digits+1)*logl(10)/logl(2));
mpfr_init2(phi, precision);
mpfr_sqrt_ui(phi, x, MPFR_RNDN);
mpfr_add_ui(phi, phi, 1.0, MPFR_RNDN);
mpfr_div_ui(phi, phi, 2.0, MPFR_RNDN);
mpfr_printf("%.10000Rf\n", phi);
mpfr_clear(phi);
唯一要注意的是 mpfr 內部用的 precision 是以 2 進位為底,所以我們在十進位需要的精確度,要先換算為 2 進位的位數,再來就能直接算出 phi 啦,
試著算過 50000 位數再對個網路上找的答案
,數字是完全一樣的。
這個 library 算得非常快,一百萬位的 phi 也是閃一下就出來了,一億位在我的 64 bit Linux, 2 GHz AMD Ryzen 5 需時 37s,
相比 e, pi 這類超越數,phi 只需要 sqrt(5) 真的是非常簡單的了。
扯遠了拉回來,如果我們要用 mpfr 這個函式庫,利用公式解來算 fib(93),要怎麼做呢?
fib(93) 到底有多少位數呢?
我們可以用 2^n 作為 F(n) 的上界
,
最後所需的位數至少就是 ceil(n*log(2)),相對應的我們運算中的浮點數精確度的要求,2^n 這個上界有點可恥粗糙但有用,
頂多會浪費點記憶體,最後除出來的小數點後面多幾個零而已,如果能套用更精確的上界當然更好。
mpfr 的函式庫設計精良,呼叫上非常直覺,這段程式碼其實就是寫公式解,應該滿好懂的,
程式碼在此
。
有了這個就可以亂算一堆 fib 了,基本上要算費式數列第一億項 fib(100,000,000) 也是 OK 的(好啦我不保證答案是對的XD,至少 fib(10000) 是對的)。
But,人生最厲害的就是這個 But,公式解真的有比較快嗎?
我個人認為答案是否定的,我們同樣可以用 fast-fibonacci 搭配 gmp 函式庫來計算,因為都是整數的運算可以做到非常快,
我的測試程式碼在此
:
同樣是計算 fib(100,000,000):
| user | system | total | |
|---|---|---|---|
| formulafib.c | 57.39s | 2.04s | 1:01.09 |
| fastfib.c | 4.70s | 0.20s | 6.524 |
O(lg n) 的 fast-fibonacci 遠比 O(1) 的公式解來得快。
問題就在於,到了所謂的大數區域,本來我們假定 O(1) 的加法、乘法都不再是常數時間,而是與數字的長度 k (位元數)有關。
而上面我們有提到,基本上可以用 2^n 作為費式數列的上界,也因此費式數列的數字長度 k ~= n,加法、乘法複雜度就會視實作方式上升到 O(n) 跟 O(n^2) 或 O(n lg n) 左右。
在 fast-fibonacci,我們需要做 lg n 次的 iteration,每次三個乘法兩個加減;
公式解雖然沒有 iteration,但需要計算兩次次方運算,也等於是 lg n 次的乘法跟加法,然後還有除法,我們運算的又不是整數而是浮點數,
這又需要更多的成本,一來一往之間就抵消了公式解直接算出答案的優勢了。
在通常的應用上以及現今電腦的實作,我們還是可以假設整數的加減乘都能在近乎常數時間內結束,這樣我們才能好好討論資料結構與演算法的複雜度,進而把複雜度學好。
費氏數列的問題在於,在數字小不用考慮運算複雜度的時候,公式解和 O(lg n) 的 fast-fibonacci 看不出差異,等到 n 終於大到看得出 O(lg n) 跟 O(1) 的差異時,已經要把運算複雜度納入考量了。
理論上我們當然可以假設有個計算模型,無論有多少位的數字,無論浮點數有多少精確度要求,四則運算與次方都能在常數時間內結束,
這時公式解就能來到 O(1),但這樣的假設不像停機問題假設的萬能機器,在學術討論上看來不太有意義。
利用 gmp, mpfr 這樣的函式庫,插滿記憶體甚至把硬碟當記憶體來用、把記憶體當 cache 用,浪費幾個星期跟一堆電力, 我們可以把無理數算到小數點下一億位、十億位,這是前人們精心為我們建的巨塔,可是數字還是無窮無盡, 站在巨塔上反而才看得出我們跟無限有多麼遙遠,誠然人腦可以透過思考一窺數學之奧妙, 但不代表我們能超脫數學的嚴格限制浮空而起,妄想記錄無限,我認為是對數學的一種褻瀆。
看了這麼多碎碎念大家想必也累了,總而言之本文透過兩個實作,讓大家體會一下所謂 O(1) 公式解並不一定是 O(1),背後一定有對應的成本; 還有就是把費式數列算到一億位真的有點爽,不過我想是沒什麼公司在實務上有在賣 fibonacci 相關的產品啦, 除非你想像日本一樣出個寫滿 e, pi 到一百萬位的書 讓人當亂數表來用。