上一回設定好 testbench 之後,終於可以來寫 verilog 了,這回就來看看我們怎麼用我們這套 Testbench, 搭配 verilog 的 pipeline 設計來實作 RSA256。
Pipeline
首先先從 pipeline design,所謂 pipeline 是在 verilog 上面建構控制訊號的抽象化, input/output 各是一組 valid ready 來控制,內含極少量的 logic,比較大的模組就能像堆積木一樣一層一層往上堆。
我們在 RSA256 所用到的 pipeline design 及其描述,包括以下幾個:
| Module | Description |
|---|---|
| Pipeline | 是的這個 module 就叫 pipeline,它控制有 data 要敲一級 Pipeline 這件事,通常會用在一個 module 的最前端,上一級給資料我就先存下來 |
| PipelineFilter | 過濾資料,透過外接的 i_pass 訊號,控制輸入資料要不要送去輸出 |
| PipelineDistribute | 一對多驅動多個模組,一次驅動後要等待每個模組都收下才會再送下一組,分散的數量透過 parameter 來控制 |
| PipelineCombine | 收集來自多個模組的輸入整合為一個輸出,收集的數量透過 parameter 來控制 |
| PipelineLoop | 在收到 input 之後,先送出 init signal,接著持續驅動 output module 直到 o_done 訊號為止 |
加上這一層能有效抽象化 verilog 模組的行為,也許一時之間看不出這麼做的好處,但後面會有一個例子。
除了上述之外,還有一些控制 data 的 module 也值得做,但在 RSA 還不需要。
| Module | Description |
|---|---|
| PipelineDivider | 收 N 維的資料,分解成多組 M 維依序輸出,N > M 且 N % M = 0 |
| PipelineMerger | 收多組 N 維的資料,組合成 M 維後依序輸出,N < M 且 M % N = 0 |
| PipelineSerializer | 收 N 維的資料,切成成多組 M 維,N > M,切到最後會剩下一些剩餘,會跟下一組資料併起來再繼續切斷 |
| PipelineDeserializer | 收 N 維的資料,組合成 M 維後輸出,N < M,組合完的剩餘會接在下一組資料上繼續輸出 |
RSA256
這裡不詳述 RSA 演算法,簡單來說我們會需要算大數的模運算 $ m^k \bmod N $,其中的 m, k, N 都是 256 bits 的 integer。
因為模運算直接算等於是算除法會花很多時間,因此我們會套用 Montgomery reduction
,
每跑一次 Montgomery Reduction 就會算出 $ a \cdot b \cdot 2^{-256} \bmod N $。
接著我們可以將傳入的 m, k 的 m 包成 montgomery form:$ m \cdot 2^{256} \bmod N $, 如此一來在算 exponential,套用 square and multiply 時,就能分別計算:
- square: $REDC((m \cdot 2^{256} \bmod N) \cdot (m \cdot 2^{256} \bmod N)) = m^2 \cdot 2^{256} \bmod N $
- multiply: $REDC((m \cdot 2^{256} \bmod N) \cdot k) = m \cdot k \bmod N $
讓 square 保持在 montgomery form,multiply 則是脫殼成非 montgomery form,跑完 square and multiply 後想要的答案。
Block Diagram
本次設計的 block diagram 如下:
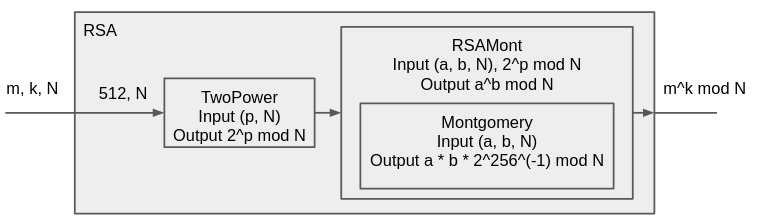
總共是四個 module,依照自訂的設計規範,我們只使用一個 Montgomery unit。
假裝一下我們有做 SCA ,在 square and multiply 的部分,我們無論 key 的 bit 是零是一都會做 montgomery,
所以會做 1 次把 m 轉成 montgomery form 及 512 次 square and multiply,共 513 次 Montgomery。
如果要加速的話,可以考慮使用兩個 montgomery,以及可以把 montgomery 每次運算的 bit 數改為 2 甚至 4。
我自己是記得當年實驗課的時候真的有強者我同學這麼幹,要知道那個時候我們都還很菜,介面沒統一,
重改一次 montgomery 等於是狀態機整個重寫,能在死線前把 RSA 寫出來就已經謝天謝地了,
能實作更快的 montgomery 真的就是只有神人才能辦到。
SystemVerilog Datatype
跟 C model 和 systemC 的 vint 一樣,SystemVerilog 支援自定義 struct 的功能,所有的型別定義放在 RSA_pkg.sv:
parameter MOD_WIDTH = 256;
parameter INT_WIDTH = 32;
typedef logic [MOD_WIDTH-1:0] KeyType;
typedef logic [INT_WIDTH-1:0] IntType;
typedef struct packed {
KeyType a;
KeyType b;
KeyType modulus;
} MontgomeryIn;
typedef KeyType MontgomeryOut;
其他 module 就能使用 import RSA_pkg::*; 來引入 systemverilog 定義。
受限於 verilator 的模疑功能,sytemverilog 的 struct 一定要使用 packed 的 struct,
這在看波形的時候所有的 bits 會糊在一起很難看,不過不算太嚴重,畢竟通常一進到模組,
就會先把 struct 拆開來放進 register 裡。
Montgomery
以下就用 Montgomery 當作範例,解釋如何使用自定義 type 與 pipeline 來完成 verilog 設計。
import RSA_pkg::*;
module Montgomery #(
parameter MOD_WIDTH = 256
) (
// input
input clk,
input rst_n,
// input data
input i_valid,
output i_ready,
input MontgomeryIn i_in,
// output data
output o_valid,
input o_ready,
output MontgomeryOut o_out
);
模組的 input/output 統一使用 valid/ready 管理,有了 struct 型別定義也輕鬆許多,幾乎所有模組的介面都是一樣的。 如下所示,把 Montgomery 拆解開來,可以把它的行為簡化成:迴圈 256 次,第 256 次時答案會算出來。
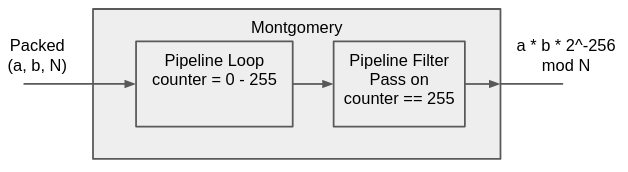
省去宣告線的部分,先宣告好這兩個模組:
PipelineLoop i_loop(
.clk(clk),
.rst_n(rst_n),
.i_valid(i_valid),
.i_ready(i_ready),
.i_cen(loop_init),
.o_valid(loop_o_valid),
.o_ready(loop_o_ready),
.o_done(loop_done),
.o_cen(loop_next)
);
PipelineFilter i_filter(
.i_valid(loop_o_valid),
.i_ready(loop_o_ready),
.i_pass(loop_done),
.o_valid(o_valid),
.o_ready(o_ready)
);
接著只要填好 loop_init、loop_next 時要做什麼,什麼時候 loop_done 就好了。 例如,在 loop_init 的時候要把 input 上的 MontgomeryIn 解開來存進 register。
always_ff @( posedge clk or negedge rst_n ) begin
if (!rst_n) begin
data_a <= 0;
data_b <= 0;
data_modulus <= 0;
end
else begin
if (loop_init) begin
data_a <= {2'b0, i_in.a};
data_b <= {2'b0, i_in.b};
data_modulus <= {2'b0, i_in.modulus};
end
end
end
這裡有一個設計上的小細節,下列兩個是二選一:
- 是要 input 敲 register,combinational circuit 接 output。
- 還是 output 接 register,input 時先過一層 combinational circuit 再進 register。
另外兩種組合,input, output 都敲 register 太過沒效率;input, output 都是 combinational 則是違反 valid/ready protocol。
我身邊大家都是選 1。
round_counter 要在 loop_init 是歸零,loop_next 時遞增。
我真心覺得 verilog/systemverilog 沒有 \x -> log2(x+1)-1 這個函式很廢,明明使用率這麼高。
// round_counter
logic [$clog2(MOD_WIDTH+1)-1:0] round_counter;
always_ff @(posedge clk) begin
if (loop_init) begin
round_counter <= 0;
end
else if (loop_next) begin
round_counter <= round_counter + 1;
end
end
round_counter 會從 0 數到 255 了,用 round_counter 去取 a 的 bit,計算出要更新的值。
always_comb begin
if (loop_done) begin round_result_next = round_result; end
else begin
round_result_next = round_result;
if (data_a[round_counter]) begin
round_result_next = round_result + data_b;
end
if (round_result_next[0]) begin
round_result_next += data_modulus;
end
round_result_next >>= 1;
end
end
最後像輸出的 combinational circuit 以及 loop_done 都可以用 assign 實作:
assign mod_result = round_result > data_modulus ?
round_result - data_modulus : round_result;
assign o_out = mod_result[MOD_WIDTH - 1 : 0];
logic loop_done = round_counter == MOD_WIDTH;
如此一來就能十分結構化的完成 module 設計,不用明寫整個狀態機,把背後的控制邏輯交給已經驗證過的 pipeline 處理。
Pipeline Example
這裡有另一個例子,說明使用 Pipeline 的好處,在實作 RSA Top module 的時候,曾在打多筆測資時驗到一個 bug。
原因是我在第一級的 pipeline 上把 m, e, N 存下來,N 會立刻送去 TwoPower 計算 $ 2^{256} \bmod N $,
TwoPower 打包完會跟 m, e, N 整團送去 RSAMont。
而如果 RSA 的 input 擺著下一筆資料要送,就會形成新資料 m’, e’ 蓋掉 m, e 送進 RSAMont,結果當然不是對的。
修正在有 pipeline 下也很簡單,和 TwoPower 並聯一組 Pipeline,前後用 Distribute 和 Combine 連接, 舊資料就可以保存進另一組 register,如下所示。
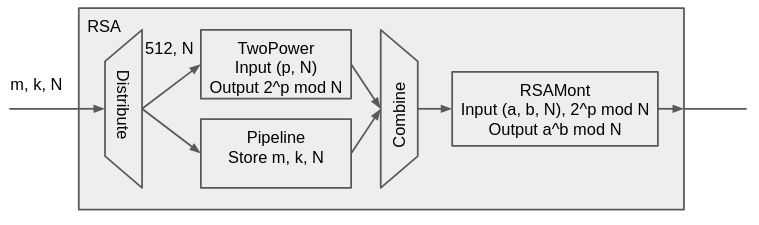
最棒的是因為 distribute 跟 combine 都是同步送與同步收,完全不用擔心該怎麼讓 Pipeline 敲一級 register 這件事, 和 256 cycle 的 TwoPower 要怎麼同步。
順帶一提,在沒用 Pipeline 的設計上,當有一個 module 要花十個 cycle,而有資料要跟它同步時,我是真的看過這樣的寫法:
reg data;
reg data_w0, data_w1, data_w2, data_w3, data_w4
reg data_w5, data_w6, data_w7, data_w8, data_w9;
always @(posedge clk) begin
data_w0 <= data;
data_w1 <= data_w0; data_w2 <= data_w1; data_w3 <= data_w2; data_w4 <= data_w3;
data_w5 <= data_w4; data_w6 <= data_w5; data_w8 <= data_w7; data_w9 <= data_w8;
end
這個寫法的擴展性就會很差,假設那個花十個 cycle 的 module 最佳化成 6 個 cycle,這整團修起來就會大費周張。
用上 valid/ready, pipeline 配個 fifo 則根本不會有這個問題,不同速度的 module 可以自動同步。
Compile and Test
目前 project 使用 verilator 搭配 verilator cmake 進行測試,設定大概如下:
set(LINKME PRIVATE SystemC::systemc glog RSASystemCModel)
add_executable(${RSA_SIM} RSA_sim.cpp)
target_link_libraries(${RSA_SIM} ${LINKME})
verilate(${RSA_SIM} TRACE_FST PREFIX VRSA SOURCES RSA_pkg.sv RSA.sv)
add_test(${RSA_SIM} ${RSA_SIM})
透過 verilate command 可以把 systemverilog 指定給測試目標;RSA_sim.cpp 則是用 testbench 實作的測試程式。
搭配 上一篇
實作的 testbench,就能很快用大量資料測試實作的 verilog 了。