故事是這樣子的,最近工作之餘頻繁地遇到 NTT 這個東西,但這個東西不是很好懂,所以想說來筆記一下, 順便用一個簡單的例子來說明 NTT/INTT 的流程與結果。
簡而言之呢,NTT 就是 Nippon Telegraph and Telephone 日本電信電話…欸不是這個 NTT ,這邊要講的是 number-theoretic transform,中文是翻數論轉換。
可以把它看成離散傅立葉轉換 DFT 的一個通用的形式,把一個數或一個多項式分解成多個選定的因子的向量;
反向的 Inverse NTT 則可以反過來從分解開來的向量再轉回去本來的元素。
為什麼要用 NTT 呢?
就像傅立葉轉換把時域的訊號轉到頻域上,讓時域的 convolution 轉成頻域直接相乘;
本來 Finite field 的 convolution ,在 NTT 轉換後可以變直接乘,對整數或多項式的乘法來說很有用。
中國剩餘定理
開始之前,我們先來講中國剩餘定理 , 中文問題描述如下:
今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?
白話翻譯就是有一個數除三餘二、除五餘三、除七餘二,求這個數?
先不管這個問題要怎麼解,想知道更多的可以看上面的 wiki 或是台大數學系的文章
。
中國剩餘定理指出的一個性質是,給我一個數 N,以及幾個互質的數 $q_0 \sim q_{n-1}$ 及這些數的乘積 Q,
只要知道 N 除以 $q_0 \sim q_{n-1}$ 的餘數,就能計算出 N/Q 的餘數;或者說,0 ~ Q-1 這 Q 個數,
除以 $q_0 \sim q_{n-1}$ 之後形成的集合都會是獨一無二的。
多項式環
這次要講的 NTT,我們會在多項式環上操作
而要構造多項式的環有兩種模運算要選擇。
第一個是多項式的模…式 Z?多半選擇 $X^N + 1$ 或是 $X^N - 1$。
第二個是係數的模數,會選一個質數或半質數 q。
這樣的多項式環符號會表示為(選用 $X^N+1$):
$$Z_q[x]/(x^N+1)$$
所以這到底是什麼意思?
第一個模式 Z,表示多項式都必須對這個模式取模。
第二個模數 q,表示所有多項式的係數都必須對這個數字取模。
下面我們就用一個玩具例子來試試,選用
$$ Z = X^4 - 1 \quad q = 5 \quad R = Z_5[x]/(x^4-1) $$
下面這個多項式就是這個多項式環的元素:$4x^3 + 3x^2 + 2x + 1$
沒有 x 的純數字當然也是了:0, 1, 2, 3, 4
只要多項式最高的次數小於 4,係數都小於 5 即可。
加法運算也是 OK 的,記得算完要取模就行了:
$(4x^3 + 3x^2 + 2x + 1) + 4 = (4x^3 + 3x^2 + 2x + 0)$
$x^4$ 呢?$x^4-1 = 0 \implies x^4 = 1$
$x^5$ 呢?$x^5 = x(x^4) = x $
有點感覺了嗎?
NTT
在 NTT 中我們會選一個 ω,使得 ω 為 (N-1) primitive root,在上面的例子我們可以選 3,可以看到在 module 5 時: $$ 3^1 = 3 \newline 3^2 = 4 \newline 3^3 = 2 \newline 3^4 = 1 \newline $$
以 3 為 ω,在這個多項式環 $Z = x^4-1$ 的元素,我們就能做個分解: $$ x^4-1 \newline = (x^2+1)(x^2-1) \newline = (x^2-\omega^2)(x^2-\omega^4) \newline = (x-\omega)(x+\omega)(x-\omega^2)(x+\omega^2) \newline = (x-\omega)(x-\omega^3)(x-\omega^2)(x-\omega^4) $$ 也就是說,本來的 Z 可以分解成 (x-1) (x-2) (x-3) (x-4) 的乘積,本來的 X 多項式, 可以表達為對這四個因式求模的時候的餘數,轉為一個四維的向量 Y,X->Y 的轉換就是 NTT,Y->X 的轉換就是 INTT。
用上述的中國剩餘定理的方式來說,就是今天遇到 105 內的數字,我們也不記是多少, 而是記下這個數除三個質數 3, 5, 7 出來的三個餘數,就能算回去本來的數字。
做個表來對照一下中國剩餘定理與此例中多項式的關係,基本上就是不同集合上的變化。
| 中國剩餘定理 | $R = Z_5[x]/(x^4-1)$ | |
|---|---|---|
| 集合 | 整數對 105 取模 | 多項式對 $x^4-1$ 取模;係數對 5 取模 |
| 列舉所有元素 | 0-104 | 最高 3 次,係數 0-4 的多項式 |
| 因式 | 3,5,7 | (x-1) (x-2) (x-3) (x-4) |
乘法操作
轉換之後,在 Y 上面做乘法就是向量與向量做內積即可,因此本來的多項式乘法 X3 = X1 * X2 變成四個步驟:
- Y1 = NTT(X1)
- Y2 = NTT(X2)
- Y3 = Y1 * Y2
- X3 = INTT(Y3)
轉換的規則如下,這部分的運算來自於餘式定理
:
$$
NTT := y_i = \sum_{i=0}^{n-1}x_i \cdot \omega^i \newline
INTT := x_i = \frac{1}{n} \cdot \sum_{i=0}^{n-1}y_i \cdot \omega^{-i}
$$
乘法實例
這裡我們就用同一個多項式環,來算 $ (4x^3 + 3x^2 + 2x^1 + 1) \times (1x^3 + 2x^2 + 3x + 4) $ $$ (4x^3 + 3x^2 + 2x^1 + 1) \times (1x^3 + 2x^2 + 3x + 4) \newline = 4x^6 + 11x^5 + 20x^4 + 30x^3 + 20x^2 + 11x + 4 \newline = 24x^2 + 22x + 24 \newline = 4x^2 + 2x + 4 $$
用 NTT 的話,我們可以把上述 NTT, INTT 寫成矩陣的形式
$$ NTT = \begin{bmatrix} \omega^0 & \omega^0 & \omega^0 & \omega^0 \\ \omega^0 & \omega^1 & \omega^2 & \omega^3 \\ \omega^0 & \omega^2 & \omega^4 & \omega^6 \\ \omega^0 & \omega^3 & \omega^6 & \omega^9 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 3 & 4 & 2 \\ 1 & 4 & 1 & 4 \\ 1 & 2 & 4 & 3 \end{bmatrix} $$ $$ INTT = \frac{1}{n} \begin{bmatrix} \omega^0 & \omega^0 & \omega^0 & \omega^0 \\ \omega^0 & \omega^{-1} & \omega^{-2} & \omega^{-3} \\ \omega^0 & \omega^{-2} & \omega^{-4} & \omega^{-6} \\ \omega^0 & \omega^{-3} & \omega^{-6} & \omega^{-9} \end{bmatrix} = 4 \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 3 \\ 1 & 4 & 1 & 4 \\ 1 & 3 & 4 & 2 \end{bmatrix} $$
首先把 X1, X2 NTT 轉為 Y1, Y2:
$$ Y1 = NTT(X1) = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 3 \\ 1 & 4 & 1 & 4 \\ 1 & 3 & 4 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \\ 3 \\ 4 \end{bmatrix} $$
$$ Y2 = NTT(X2) = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 3 \\ 1 & 4 & 1 & 4 \\ 1 & 3 & 4 & 2 \end{bmatrix} \begin{bmatrix} 4 \\ 3 \\ 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \\ 2 \\ 1 \end{bmatrix} $$
$$ Y3 = Y1 * Y2 = \begin{bmatrix}0 \\ 1 \\ 1 \\ 4\end{bmatrix} $$
$$ X3 = INTT(Y3) = 4 * \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 3 \\ 1 & 4 & 1 & 4 \\ 1 & 3 & 4 & 2 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 1 \\ 4 \end{bmatrix} = \begin{bmatrix} 4 \\ 2 \\ 4 \\ 0 \end{bmatrix} $$
得到結果同樣是 4x^2 + 2x + 4。
其他不同的變化
選用不同的 Z 與 q
上述的例子我們選用 x^4 - 1 = 0,常見形式還有另一種 x^4 + 1 = 0。
這時候因為 x^4 = -1,所以我們需要找到 primitive root 是 ω^8 = 1,因為費馬小定理,
最小的要用 q = 17,ω = 2 來做。
分解如下:
$$
x^4 + 1 \newline
= x^4 - \omega^4 \newline
= (x^2 - \omega^2) (x^2 + \omega^2) \newline
= (x - \omega) (x + \omega) (x^2 - \omega^6) \newline
= (x - \omega) (x - \omega^5) (x - \omega^3) (x - \omega^7) \newline
$$
我們可以用 (x-2) (x-8) (x-9) (x-15) 做為分解的因式。
Fast NTT
從上例來看,算乘法還要先轉去另一個 domain,乘完再轉回來不會更慢嗎?
這就要用到 FFT 的原理,把奇次項和偶次項分開來用 divide and conquer 遞迴算出結果,讓 NTT/INTT 的複雜度降到 O(n log n) ,
比直接做 convolution 的 O(n^2) 還要快;當然這是指純複雜度而言,實際上會不會比較快還是要實做才知道。
用上面的例子,我們來分解一下 $ 4x^3 + 3x^2 + 2x + 1 $
先把 x^4 - 1 = 0 拆分為 $(x^2 - \omega^2)(x^2 + \omega^2) $,同樣是用餘式定理代入 $ x^2 = 4, x^2 = 1 $
$$
4x^3 + 3x^2 + 2x + 1 \newline
= x^2 (4x+3) + (2x+1) \newline
x^2 = 4 \implies 3x+3 \newline
x^2 = 1 \implies x+4 \newline
$$
接著分解 3x+3 代入 x = ω = 3 和 x = ω^3 = 2;分解 x+4 代入 x = ω^2 = 4 和 x = ω^4 = 1。
即得到 [2, 3, 4, 0]。
可以注意到,每次分解要代入的數字一正一負,如第一輪是 ω^2、-ω^2;第二輪是 ω 和 -ω = ω^3。
且每次分解都是將多項式對半分解,高次項和 ω 的次方項相乘,一正一負和低次項組合起來。
一般會稱每次運算的 ω 的次方項為 twiddle factor,並使用所謂的 butterfly unit 來實作, 取一次 twiddle factor 就能完成一層的分解。 至於為什麼要叫 butterfly unit 就如下圖所示,只是可能需要一點想像力:
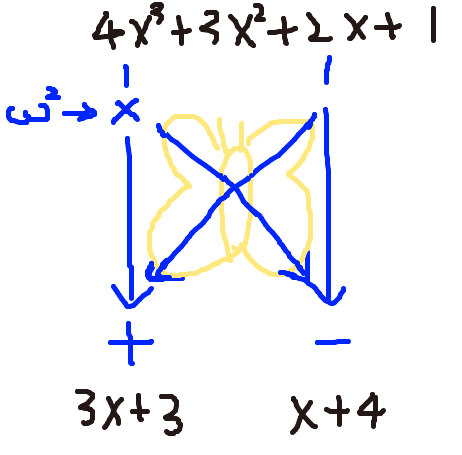 詳細可以參考 Cooley-Tukey FFT Algorithm
。
詳細可以參考 Cooley-Tukey FFT Algorithm
。
Incomplete NTT
上面提到的 generator 為 3 的,一般稱為 complete NTT,也就是所有的項次都分解成一次項了。 相對的不做到最後的 NTT 稱 incomplete NTT,出來的會是對較高項的取模。
為什麼要這麼做,因為從 Fast NTT 的例子可以看到,愈是到最後一層,要分解的次數也就愈多;為了效能考量, 如果計算次數不高的多項式乘法很快的話,也沒必要分解到最後一層,趕快乘完就轉回去了。
我們就在同一個有限體上,再算一次 $ (4x^3 + 3x^2 + 2x^1 + 1) \times (1x^3 + 2x^2 + 3x + 4) $。 如同在 Fast NTT 一節所述,只針對 x^2 去分解:
$$ (4x^3 + 3x^2 + 2x^1 + 1) \equiv (3x+3) \pmod{x^2=4} \newline (4x^3 + 3x^2 + 2x^1 + 1) \equiv (x+4) \pmod{x^2=1} \newline (1x^3 + 2x^2 + 3x + 4) \equiv (2x+2) \pmod{x^2=4} \newline (1x^3 + 2x^2 + 3x + 4) \equiv (4x+1) \pmod{x^2=1} $$
前項是 $ x^2 = 4 $;後項是 $ x^2 = 1 $;相乘得:
$$ (3x+3)(2x+2) = (6x^2 + 2x + 1) = (2x) \newline (x+4)(4x+1) = (4x^2 + 2x + 4) = (2x+3) $$
求解一個是用中國剩餘定理,先分別求得 (x^2-4) 在 mod (x^2-1) 和 (x^2-1) 在 mod (x^2-4) 下的模反元素: $$ 3 (x^2-4) \equiv 1 \pmod{x^2-1} \newline 2 (x^2-1) \equiv 1 \pmod{x^2-4} $$
得解 $$ 3 (2x+3) (x^2-4) + 2 (2x) (x^2-1) \newline = 10x^3 + 9x^2 - 28x - 36 \newline = 4x^2 + 2x + 4 $$
或者簡單一點,可以直接用反向的 butterfly unit。
低次項 = $ ((2x+3) + (2x)) / 2 = 2x + 4 $
高次項 = $ ((2x+3) - (2x)) / 2x^2 = 4x^2 $
都可以算出正確答案 $ 4x^2 + 2x + 4 $
結語
這篇文我試著解釋 NTT/INTT 是什麼,儘量用了一個簡單的例子,讓大家可以實際操作一下,
希望有讓 NTT 在幹嘛變得更好懂。
但說實話 NTT 這個題目本來就又多又雜,還有其他各種奇怪的變形跟推廣,我現在也還是一知半解,說得一口好 NTT。
致謝
本文感謝一同工作的數學系同學們的指導,不厭其煩的講解了許多次的 NTT 給我聽;以及對此文多次的校對。
同時我要感謝以下的參考資料,第一篇的例子還很剛好的選到跟我一樣的,大概大家都覺得 x^2+1 太簡單, 看不出變化所在,而用 x^4+1 最小的質數就是 17,就選到一樣的了。